Intersection point of two lines
(2 dimensions)
Written by Paul Bourke
April 1989
Sample source code
Contribution by Damian Coventry: example.cpp
This note describes the technique and algorithm for determining the
intersection point of two lines (or line segments) in 2 dimensions.
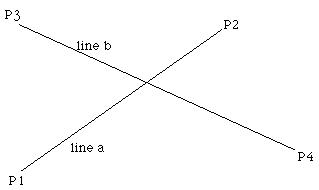
The equations of the lines are
Pa = P1 + ua ( P2 - P1 )
Pb = P3 + ub ( P4 - P3 )
Solving for the point where
Pa = Pb gives the following
two equations in two unknowns (ua and ub)
x1 + ua (x2 - x1) = x3 + ub (x4 - x3)
and
y1 + ua (y2 - y1) = y3 + ub (y4 - y3)
Solving gives the following expressions for ua and ub

Substituting either of these into the corresponding equation for the line gives the intersection point.
For example the intersection point (x,y) is
x = x1 + ua (x2 - x1)
y = y1 + ua (y2 - y1)
Notes:
- The denominators for the equations for ua and ub are the same.
- If the denominator for the equations for ua and ub
is 0 then the two lines are parallel.
- If the denominator and numerator for the equations for ua and ub
are 0 then the two lines are coincident.
- The equations apply to lines, if the intersection of line segments is
required then it is only necessary to test if ua and ub lie between 0 and 1.
Whichever one lies within that range then the corresponding line segment
contains the intersection point. If both lie within the range of 0 to 1 then
the intersection point is within both line segments.
|